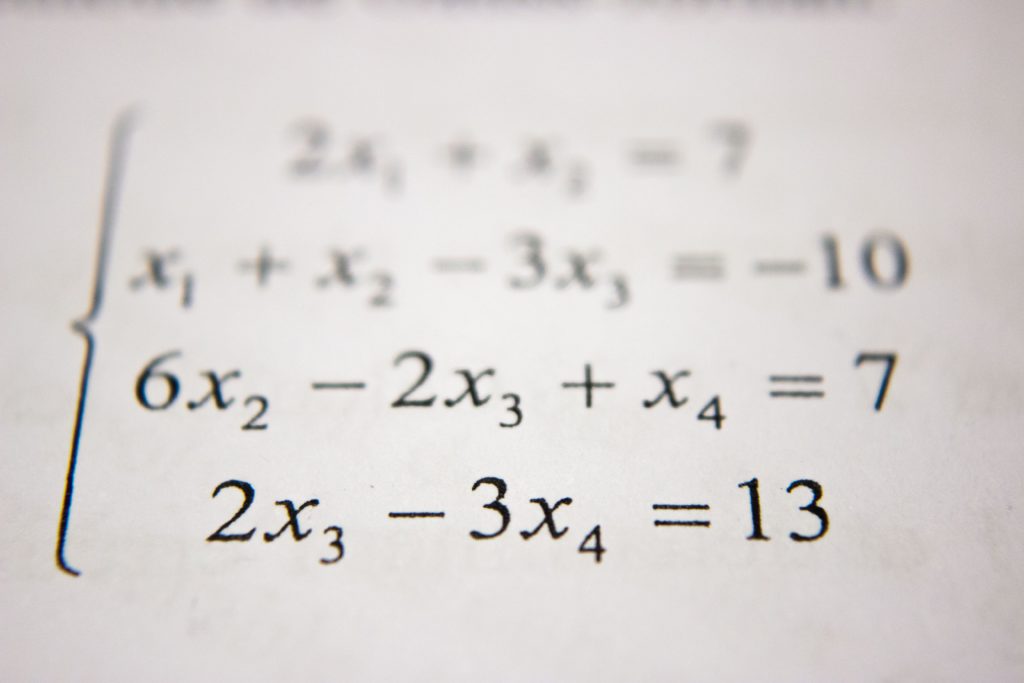どうも、さやです
いまちょこっと話題になっている話があるので検証してみました
なんと、πが「4」だという証明がでてきたというのです
昔、3.1415…とか言ってたアレです
そんなまさか、4なわけないだろおおと思いつつ気になって色々調べたので、「円周率=4」のナゾについて解説してきます
もくじ
π=4になる証明
最初に、チラっと「なぜこんな話がでてきたか?」を解説してきます
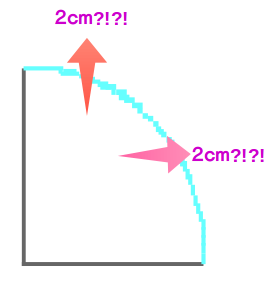
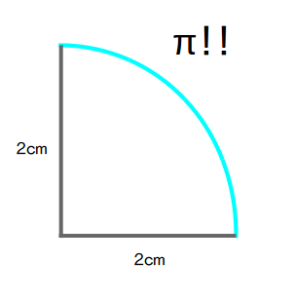
当然、半径2で、90°の弧の長さはπ
中学生で何度も見たこの図形ですね
まさか、大学生になってから扇型をまじまじ見つめることになるとは…
この青の部分の長さはズバリ、2(半径)×2÷4(等分)×πで…計算すると『π』になりますね
まあもしそんなんわすれたわって人いたら、「円の公式」とかでググってください
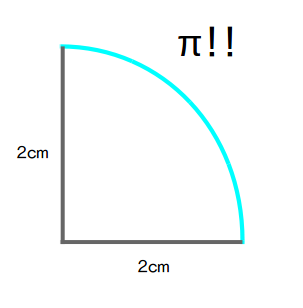
半径2で、90°の弧の長さが『4』に?!
なんとびっくり、この「青の部分」実は『4』だったことがわかっていまいます
(ちなみに、センチメートルの単位あったりなかったりややこしいねんって思った人多いかもしれないけど、見やすさ重視したから許して!!)
順番にみていきましょう
① 外側を2(cm)の枠で囲う
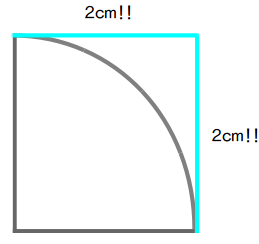
まずは、単純に、2(cm)の線を上と右に置きます
とうぜん青の線って合わせると……?
そうです、4(cm)ですね
② 折り曲げても4(cm)のまま長さは変わらない
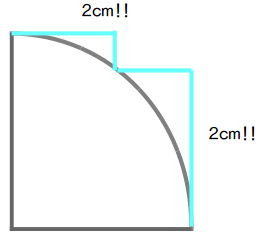
では、この緑の線の長さは何でしょうか?
もちろん4(cm)です
『ただ折り曲げただけですから』!!

2回折り曲げても、長さは変わりません
③ 無限回折り曲げると円になる?!
じゃあ、もっともっと折り曲げてみましょう
1億、1兆、1京、、、無限に!!
折り曲げまくれば、形は円に近づきます
なんせ無限回ですからね
あれ? よくみると……..青の部分って当然、4(cm)ですよね
そしてこの図を思い出してください
もう気づきましたよね
πは4なのです!!!!
これで、円周率=4という証明がなされたということなのでしょうか?
なぜ『π=4』という答えがでてくるのか
ここで、みなさんシンキングタイムです
なぜπ=4になってしまうのでしょうか?
もっと考えたいって人は携帯を一旦置いて、うんうんうなってください
(ネタバレしちゃうので!)
さすがに、円周率が4なわけはない
まあ、冷静に考えると『円周率=4』間違えですよね
もしこれが事実なら世界はひっくりかえります
でもでも確かに、ちゃんと円になってるし……..たしか円の面積の公式求める時って、なんか無限に切り分けるとかいう話もあったような………..
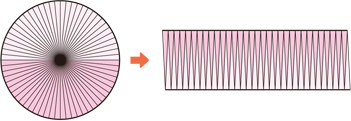
たしかに、コレとなんとなく似てますよね
では、なぜ円周率=4になるのか?!?!
無限の倍率で「拡大」したら見えてくる!!
結論から、いうと、いくら折り曲げて円っぽくしても、『限りなく小さな凸』が『無限個』あるから、円の長さに近づくことはありません
(下のはめちゃくちゃ拡大した図)
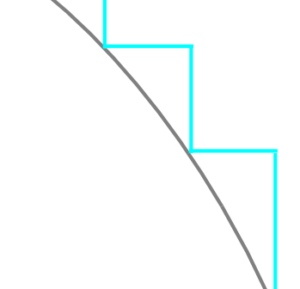
たしかに、一つ一つの凸の長さと、円の部分の長さの違いはめちゃくちゃちーーーーちゃいです
でも、そのちーーーーーちゃい差が、結局無限個あるのです
チリも積もれば山となる……………まさにこの表現が正しいですね笑笑
一向に、πと4の長さの違いは埋まることがないのです
近いようで遠い存在というのが綺麗な表現ですね(自称)
たしかに、円に対してめちゃくちゃ距離は近いです!!(人間の目では判断できないほどです)
ただ、性質はまったく別……..なんだかおもしろいですね
まとめ 円周率が4の問題解明
ふわっとした感じの説明でしたがいかがだったでしょうか?
私的には、めっちゃおもしろいなと思いました
人間の感覚ってなかなかへぼいなとも感じましたし
思いついた人ナイス!!(URLは下です)